Theory of Light and Color

28. Color Temperature and Dominant Wavelength
In the previous chapter, we introduced the concepts of color temperature and correlated color temperature. This time, we will explain their relevance to lighting in our living spaces. Additionally, while (correlated) color temperature is only applicable to white light sources, there is a similar need for a value to associate with the approximate hue of a colored light source. So this chapter will also explain dominant wavelength, which serves as a way to represent colored light sources.
(1) Psychological Effects of (Correlated) Color Temperature
Two elements that influence the effect of artificial light sources in a space are the color of the lighting (correlated color temperature) and its brightness (illuminance). The combination of these two greatly changes the psychological impression we experience.
It is well known that visually (through color), we psychologically feel a sense of temperature. ≪1≫ Regardless of the actual physical temperature of an object, colors in the red-orange spectrum give a sense of warmth, while blues and blue-violets evoke a feeling of cold. Lighting with a low (correlated) color temperature appears reddish and feels psychologically warm while lighting with a high (correlated) color temperature appears blueish-white and feels psychologically cold. It is important to note that the (correlated) color temperature value and the psychological sensation of warmth and coolness have an inverse relationship.
The diagram on the right shows the effects of (correlated) color temperature and illuminance on human psychology.
Lighting with a high (correlated) color temperature that appears white to blue-white can create a gloomy atmosphere when dim. However, if the illuminance is high, the same hue is energizing.
Conversely, lighting with a lower (correlated) color temperature that appears reddish at low illuminance can create a psychologically calm and soothing atmosphere. However, if the illuminance becomes too high, it can result in a harsh light.
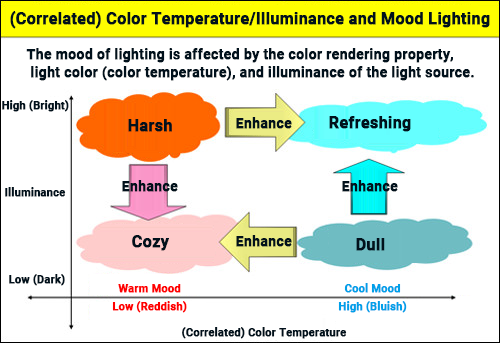
Thus, when evaluated in terms of psychological comfort, the combination of (correlated) color temperature and illuminance can have opposite effects.
(2) Fluorescent Lamp Colors
As mentioned above, lighting has a strong impact on human psychology, which is why different colors are used to achieve certain effects. For example, there are multiple types of fluorescent lamps available based on differences in correlated color temperature from 6500 K to 2700 K. (See figure right). ≪2≫
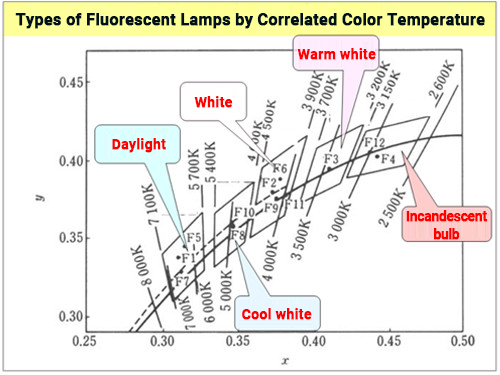
The principle of emission for fluorescent lamps involves generating ultraviolet radiation through a discharge between electrodes in a tube filled with mercury vapor, which then excites phosphors coated on the tube wall, producing visible light (fluorescence). (The ultraviolet components used for fluorescent excitation are cut off, so they do not leak outside the tube.) By selecting the type of phosphor, it's possible to alter the spectral distribution of fluorescent emission and produce fluorescent lamps in various colors.
While LEDs can be categorized similarly to fluorescent lamps, they also have unique classifications due to the nature of their manufacturing process. ≪3≫
(3) Reciprocal Color Temperature
While (correlated) color temperature is useful for representing the color of white light with a single value, it cannot adequately express color difference between multiple white lights using the difference in (correlated) color temperature values expressed in Kelvins (K). This is because the scale on the blackbody locus converges and becomes denser as the color temperature value increases.
For two white lights with a (correlated) color temperature difference ΔTCP = 100 K, for example, the color difference ΔE1 between 10,000 K and 10,100 K and color difference ΔE2 between 3,000 K and 3,100 K are quite different, with ΔE1 < ΔE2. This is because the relationship between temperature difference and color difference on the blackbody is not a simple proportional relationship.
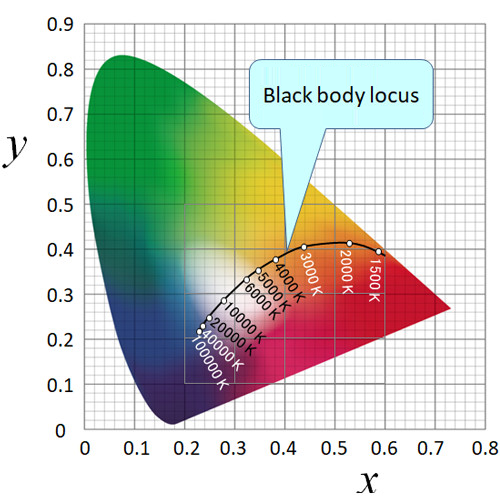
An index called the reciprocal (correlated) color temperature was developed to express color differences between white lights with respect to (correlated) color temperature values. The reciprocal (correlated) color temperature is defined as one million times the inverse of the (correlated) color temperature (unit: mrd or mrk). ≪4≫

For example, the reciprocal color temperature of standard illuminant A with a color temperature TC = 2,856 K is TC-1 = 106 / 2856 = 350.1 mrd, and the reciprocal correlated color temperature of standard illuminant D65 with a correlated color temperature
TCP = 6,504 K is TCP-1 = 106 / 6504 = 153.8 mrd. ≪5≫
The space in which reciprocal (correlated) color temperatures are displayed can generally be considered a uniform color difference space, and the relationship between the difference in reciprocal (correlated) color temperature ΔTC-1 (ΔTCP-1) and color difference ΔE becomes mostly independent of the absolute value of the (correlated) color temperature.
A reciprocal color temperature difference of approximately 5.5 mrd or less is considered indistinguishable to the human eye, regardless of the (correlated) color temperature value.
(4) Dominant Wavelength (λd)
The concept of (correlated) color temperature is widely used for its convenience, but its application is limited to white light sources. When it comes to colored light sources like monochromatic red or green LEDs, although using two values (x, y) expresses the emission color objectively and accurately, it's not easy for people to associate those two numbers with the actual color. Dominant wavelength is a practical way to approximate the color with a single number.
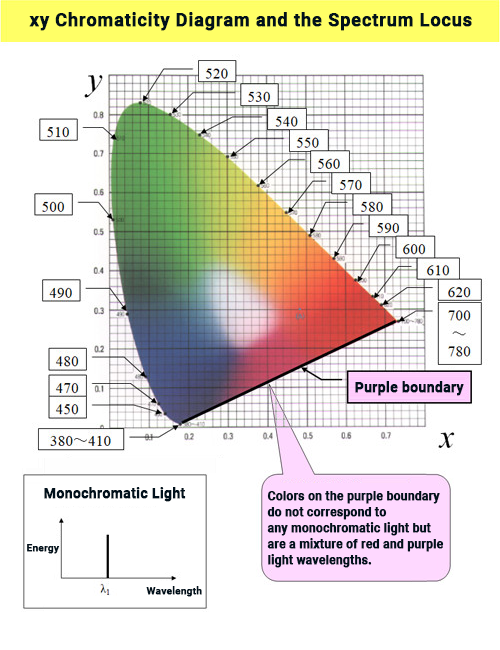
For example, in the xy chromaticity diagram below, there is a color F at (0.32, 0.51). Drawing a straight line from the white point W (0.333, 0.333) towards F and extending it further, it will eventually intersect with the spectrum locus. Let's call this point S. This point S corresponds uniquely to the chromaticity of a monochromatic light of a certain wavelength, so this wavelength is taken as the dominant wavelength (λd) of color F. (In the diagram below, point S corresponds to the chromaticity point of 550 nm monochromatic light, so the dominant wavelength of color F would be 550 nm.) The colors of monochromatic light are familiar to everyone as they line up in the order of colors of a rainbow, and it is relatively easy to associate a wavelength with a color, so hearing the value of the dominant wavelength allows us to immediately imagine what color it represents. ≪6≫
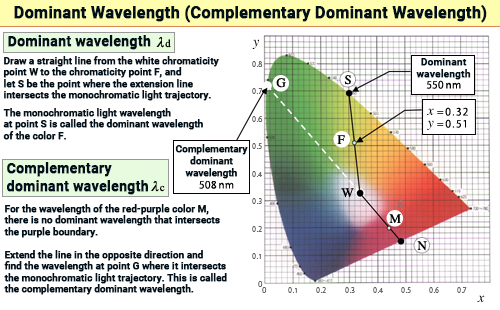
(5) Complementary Dominant Wavelength (λc)
We used the color F as an example earlier. Now consider color M at (0.44, 0.20). Extending a line from the white point W (0.333, 0.333) towards point M and beyond, it will hit not the spectrum locus but the purple boundary on the xy chromaticity diagram.
At the intersection point N with the purple boundary, there isn't a corresponding monochromatic light as with color F. In such cases, if we extend this line in the opposite direction, it hits the spectrum locus at point G. Since a certain wavelength of monochromatic light corresponds uniquely to point G, we take this wavelength as the complementary dominant wavelength (λc) of color M. In the diagram, point G corresponds to the chromaticity of 508 nm monochromatic light, so the complementary dominant wavelength of color M is 508 nm.
It's difficult to "directly" associate the value of the complementary dominant wavelength (λc = 508 nm) with color M, but by being aware of the relationship of complementary colors, it's possible to indirectly associate M. As you may understand from Chapter 25, since the xy chromaticity diagram is a linear space, colors that exist diametrically opposite around the white point W have a precise complementary relationship (when mixed in the appropriate ratio, they produce an achromatic color).
In the diagram above, with our understanding of complementary relationships, we know that the chromaticity point lies within the triangle region on the xy chromaticity diagram that uses the purple boundary as the base and the white point W as the apex – that is, within the range of purple to red-purple to red colors. Then, knowing that 508 nm monochromatic light is green, we can infer that the chromaticity point is in the red-purple (magenta) color spectrum.
As illustrated above, the dominant wavelength and complementary dominant wavelength can be said to correspond to hue, which is one of the three psychological attributes of color.
(6) Exciting Purity (pe and pec)
All the chromaticity points lying on (and extending beyond) the line that connects a color and the white point W have the same value of dominant wavelength (or complementary dominant wavelength). In other words, all colors on this line have the same hue.
As discussed in Chapter 23, chroma increases radially outward from the white point W on the xy chromaticity diagram. Exciting purity represents saturation using the relative ratio of the distance from W to the spectrum locus or purple boundary (WS or WN) in comparison to the distance from W to the chromaticity point (WF or WM).
Note that in the case of the complementary dominant wavelength, the line from the white point W to the color M was extended in the opposite direction, but for exciting purity, the intersection with the purple boundary point N and the white point W's distance is considered 100%.
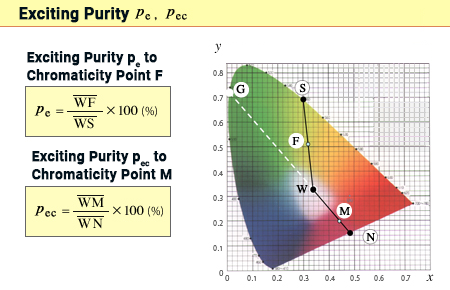
Colors on the outer edge (spectrum locus and purple boundary) of the xy chromaticity diagram all have an exciting purity of 100% - the highest saturation, while the white point W has an exciting purity of 0% - the lowest saturation (achromatic).
(7) Dominant Wavelength (Complementary Dominant Wavelength) Notation and Color Temperature (Correlated Color Temperature) Notation
As mentioned above, the definitions of dominant wavelength (or complementary dominant wavelength) are entirely different from those of color temperature (correlated color temperature). However, both are convenient ways to associate a color with a single value. Another thing they have in common is that an additional value can be paired to accurately denote the color — deviation from the blackbody locus (duv) for correlated color temperature (TCP) notation, and exciting purity (pe or pec) for dominant wavelength λd (complementary dominant wavelength λc) notation.
The difference between the two lies in their complementary applications: (correlated) color temperature only applies to the white regions near the blackbody locus, while (complementary) dominant wavelength is for the chromatic area. ≪7≫
Comment
≪1≫ Synesthesia
Synesthesia refers to the phenomenon where a sensory reaction is triggered that belongs to a different sensory modality than the one being stimulated. Warm and cool colors, which were discussed in the text, are classic examples of this.
≪2≫ Correlated color temperature categories for fluorescent lamps
In Japan, as described in the text, five types of fluorescent lamps are commercially available (JIS Z 9112:2012), but other countries may have different categories. For example, in the United States, the nominal correlated color temperatures range from 6500 K to 2700 K and are divided into six stages.
(ANSI C78.376-2001 Specifications for the Chromaticity of Fluorescent Lamps)
≪3≫ Correlated color temperature categories in solid-state lighting
In recent years, there seems to be a shift in the categorization of correlated color temperatures in solid-state lighting, such as LEDs, which have seen remarkable development and popularity.
For example, the American National Standards (ANSI NEMA ANSLG C78.377-2011 Specifications for the Chromaticity of Solid-State Lighting Products) aim to align as closely as possible with the traditional fluorescent lamp categories while accounting for specific manufacturing considerations (such as yield) in solid-state light sources. This has led to the addition of different categories and modifications in the number of stages to eight, some of which include changes in nominal correlated color temperature values. The methods for specifying allowable chromaticity ranges have also been modified.
≪4≫ Units for reciprocal (correlated) color temperature
mrd: micro-reciprocal-degree, pronounced as mired
mrk: micro-reciprocal-Kelvin, pronounced as mirek
≪5≫ Standard illuminants A and D65
Standard illuminants are internationally agreed-upon spectral distribution characteristics of light used for observing object colors. Standard illuminant A represents a thermal radiation light source, and D65 represents daylight (daytime sunlight). Their spectral distribution characteristics are precisely defined numerically (see Chapter 23).
≪6≫ Main wavelength λd and peak emission wavelength λp
It’s important to note that the meaning of dominant wavelength λd is sometimes mistakenly used in the sense of peak emission wavelength λp.
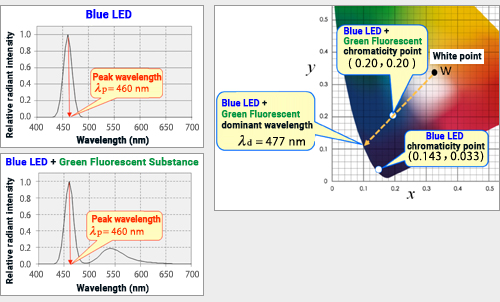
The peak emission wavelength λp refers to the wavelength where the light source's spectral distribution physically peaks in output. Therefore, it doesn't necessarily correlate with the color of the light source as the shape of the spectral distribution characteristics at other wavelengths does not matter. However, the dominant wavelength λd is determined based on the color of the light source, that is, the chromaticity point (x, y). Even if two light sources have the same physical peak emission wavelength λp, if their emission colors (spectral distribution shapes) differ, their dominant wavelengths λd will vary.
≪7≫ Applying dominant wavelength notation to object color
There is another difference in the application of color temperature and dominant wavelength notation. While color temperature notation can only be applied to light source colors (white light), dominant wavelength notation can be applied to both light source colors and object colors. For light source colors, the white point W is set at (0.333, 0.333). For object colors, however, the color of the object changes depending on the spectral distribution characteristics of the illuminating light, so the chromaticity point of the standard illuminant itself is considered the white point W. This approach considers how the light source color influences the hue direction of the object color.

